Dutos e Flanges
Considere um fluido incompressível, de massa específica \(\rho\), que escoa em regime permanente com velocidade uniforme \(v\) em um trecho de duto consistindo de uma curva a 90º, no plano horizontal, tendo uma extremidade rigidamente flangeada e outra acoplada a uma junta de expansão (veja Figura 2). Deseja-se determinar os esforços presentes no flange, admitindo desconsideráveis os esforços na junta de expansão e o peso do fluido em face das outras forças envolvidas.
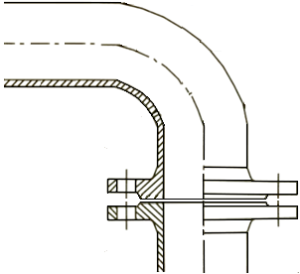
Escoamento em um duto com curva de 90°
Agora vamos fazer uma análise de um fluido incompressível escoando em regime permanente através de duto com uma curva de 90°, considerando efeitos hidrodinâmicos, térmicos e estruturais. O sistema consiste em um duto horizontal com flange rígido na entrada e junta de expansão na saída.
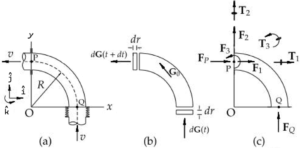
1. Definição do Problema
-
Fluido incompressível: Massa específica 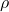\(\rho\)=constante em regime isotérmico.
-
Regime permanente: As propriedades do escoamento não variam no tempo.
-
Velocidade uniforme \(v\): A velocidade é a mesma na entrada e na saída (assumindo área transversal constante).
-
Plano horizontal: Forças gravitacionais são desprezíveis.
-
Junta de expansão: Não transmite esforços (livre para se mover).
-
Flange rígido: Transmite todos os esforços para a estrutura.
2. Equações
2.1. Conservação da Massa:
\begin{equation}
\int \rho \vec{v} d \vec{A} = \rho A (\vec{v_e} – \vec{v_s}) = 0
\end{equation}
2.2. Conservação da Quantidade de Movimento Linear:
A equação integral da conservação da quantidade de movimento para um volume de controle (VC) fixo é:
\begin{equation}
\sum \vec{F} = \int_{VC} \rho \vec{v} (\vec{v} \cdot \vec{n}) d \vec{A} = \dot{m}(\vec{v_e} – \vec{v_s})
\end{equation}
Onde:
\(\sum \vec{F}\): Forças externas atuando no \(VC\) (pressão e reação no flange).
\(\vec{F}\): Vetor velocidade.
\(\vec{n}\): Vetor normal à superfície de controle (apontando para fora).
\(\dot{m}=\rho v A\): Vazão mássica
\(\vec{v_e} = v_e \hat{i}\) e \(\vec{v_s} = v_s \hat{j}\): Velocidades na entrada e saída.
A força exercida pelo fluido no duto (ação) é:
\(\vec{R}_{flange} = \dot{m}(\vec{v_e} – \vec{v_s}) + (p_e A \hat{i} + p_s A \hat{j})\)
Se \(p_e=p_s=p\) e \(v_e = v_s = v\)
\(\vec{R}_{flange} = \rho v A(v\hat{i} – v\hat{j}) + (pA \hat{i} + pA \hat{j})\)
\(\vec{R}_{flange} = \rho v^2 A(\hat{i} – \hat{j}) + pA(\hat{i} + \hat{j})\)
A força resultante no flange é:
\[
\boxed{\vec{R}_{flange} = – (\rho v^2 + p ) A (\hat{i} + \hat{j})}
\]
2.3. Caso com Variação de Área ou Velocidade
Se a área da seção transversal mudar (\(A_e \ne A_s\)), a velocidade também muda (\(v_e A_e=v_s A_s\)), por continuidade). A equação de Bernoulli pode ser usada para relacionar pressões:
\begin{equation}
p_e + \frac{1}{2+}\rho {v_e}^2 =p_s + \frac{1}{2+}\rho {v_s}^2 +\Delta_{perdas}
\end{equation}
Onde \(\Delta p_{perdas}$ são perdas por atrito e turbulência.
Forças resultantes atualizadas:
\(R_x = \rho {v_e}^2 A_e −p_e A_e\)
\(R_y=\rho {v_s}^2 A_s −p_s A_s\)
Aplicação Prática: Dimensionamento do Flange
Para garantir a resistência do flange, um engenheiro deve considerar:
Força estática máxima:
\(R_{max} = \rho v^2 A + p A\) (considerando pressão e velocidade máximas operacionais).
1. Fator de segurança: Multiplicar \(R_{max}\) por um coeficiente.
2. Material e parafusos: O flange deve ser fabricado com material resistente (aço carbono, aço inox) e os parafusos devem ser dimensionados para suportar a carga.
3. Vibrações e fadiga: Se o escoamento for pulsante, deve-se avaliar efeitos dinâmicos.
3. Conservação do Momento Angular
3.1. Momento Torsor (Torque) no Flange
Além da força resultante, a curva pode induzir um momento torsor no flange devido à distribuição assimétrica de pressões e velocidades.
A equação integral para o momento angular é:
\begin{equation}
\sum \vec{M}_{ext} = \int \rho (\vec{r} \times\vec{v})(\vec{v}\cdot d \vec{A})
\end{equation}
- Para uma curva simétrica e flange rígido:
Como o escoamento é simétrico e o flange está rigidamente fixado, o torque líquido no flange é zero em condições ideais. Porém, em situações reais (escoamento turbulento, assimetrias), pode haver um pequeno torque residual.
Entrada: Momento angular \(-\rho r v^2A \hat{k}\).
Saída: Momento angular \(+\rho r v^2 A \hat{k}\).
Assim:
\begin{equation}
\sum \vec{M}_ext = \int \rho (\vec{r} \times\vec{v})(\vec{v}\cdot d \vec{A} = 0
\end{equation}
\[
\boxed{\vec{T} = 0}
\]
-
Com assimetria (ex.: junta excêntrica em z):
O torque \(\vec{T}\) em relação ao centro da curva é dado por:
\begin{equation}
\vec{T} = \vec{r_e}\vec{F_e} \times \vec{r_s}\vec{F_s}
\end{equation}
Onde:
\(\vec{r_e}\) e \(\vec{r_e}\) são vetores posição dos pontos de aplicação das forças.
\(\vec{F_s}\) e \(\vec{F_s}\) são as forças de pressão e quantidade de movimento nas seções de entrada e saída.
Torque no flange:
\[
\boxed{\vec{T}= – (\rho v^2 + p) r A \hat{k}}
\]
onde \(r\) é a distância do centro de curvatura ao ponto de aplicação da força.
4. Ajustes para Cenários Reais
Perdas por Atrito e Queda de Pressão
Em sistemas reais, o atrito entre o fluido e as paredes do duto causa perdas de energia, levando a uma queda de pressão ( \(\Delta p\) ). Isso pode ser modelado pela equação de Darcy-Weisbach ou por correlações empíricas.
Equação de Darcy-Weisbach:
\begin{equation}
\Delta p = f \frac{L}{D} \frac{\rho v^2}{2}
\end{equation}
Onde:
\(f\): Fator de atrito (depende do regime de escoamento e rugosidade da parede).
\(L\): Comprimento da curva ou trecho analisado.
\(D\): Diâmetro hidráulico do duto.
Impacto no modelo:
A pressão na saída (\(p_s\)) será menor que na entrada (\(p_e\)):
\(p_s = p_e – \Delta p\)
A força resultante no flange deve incluir essa diferença:
\[
\boxed{\vec{F}_{flange} = -[(\rho v^2+p_e)A \hat{i} +(\rho v^2+p_s)A \hat{j}]}
\]
Distribuição Não Uniforme de Pressão
Em curvas reais, a pressão não é constante ao longo da seção transversal devido a efeitos centrífugos:
Parede externa: Pressão mais alta.
Parede interna: Pressão mais baixa (efeito de sucção).
Modelo para Pressão Assimétrica:
A pressão pode ser aproximada por uma distribuição parabólica:
Onde:
\(\theta\): Ângulo ao longo da curva (0° a 90°).
\(\Delta p_{max}\): Diferença máxima de pressão (empiricamente determinada).
A força de pressão agora requer uma integração angular:
\begin{equation}
\vec{F}_p=\int_{0}^{\pi/2} p (\theta) \cdot \vec{n} (\theta) r d\theta
\end{equation}
Isso pode introduzir torques adicionais se a distribuição não for simétrica.
Turbulência e Vórtices
– Escoamentos reais em curvas geram vórtices secundários e turbulência, que:
– Aumentam as perdas de energia.Podem causar vibrações no duto e no flange.
Modelagem via Número de Reynolds (\(Re$):
\begin{equation}
Re=\frac{\rho v D}{\mu}
\end{equation}
Se \(Re> 4000\) escoamento é turbulento, e o fator de atrito \(f\) deve ser ajustado (usando, por exemplo, o diagrama de Moody).
Variação de Área ou Velocidade
Se o duto tem áreas diferentes na entrada ( \(A_e\) ) e saída (\(A_s\)), a velocidade muda (\(v_e A_e = v_s A_s\)), afetando o balanço de momento.
-
Conservação da massa com áreas diferentes:
\( v_s = v_e \frac{A_e}{A_s}\)
-
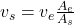
Força no flange:
Conservação da massa com áreas diferentes: \( v_2 = v_1 \frac{A1}{A2} \)
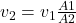
Força resultante atualizada:
\begin{equation} \vec{F} = -[(\rho {v_1}^2 + p_1)A_1 \hat{i} + (\rho {v_2}^2 + p_2)A_2 \hat{j}] \end{equation}
Efeitos Dinâmicos Transiente
Em cenários como fechamento de válvulas ou partida do sistema, forças adicionais surgem devido a acelerações do fluido.
Equação de Momentum Transiente:
\begin{equation} \vec{F}_{inercia} = \rho L A \frac{\vec{F}}{dt} \end{equation}: Comprimento característico do duto.
\(\frac{dv}{dt}\): Aceleração do fluido.
Variação das Propriedades do Fluido com a Temperatura
Para líquidos (ex.: água, óleo) e gases (ex.: ar, vapor), \(\rho\) e \(\mu\) dependem da temperatura (\(T\)):
-
Líquidos:
\(\rho (T)= \rho_0[1 – \beta(T – T_0)]\), \(\mu(T) \propto e^{-k(T – T_0)}\)
(\(\beta\) = coeficiente de expansão térmica, \(k\) = constante empírica).
- Gases (lei dos gases ideais):
\(\mu (T) \propto T^{0.7}\)
Dilatação Térmica do Duto
O material do duto (aço, PVC, etc.) expande-se com a temperatura:
\begin{equation} \Delta L=\alpha L \Delta T \end{equation}= coeficiente de dilatação térmica.
Critério de falha:
Tensão térmica:
\(\sigma_{termico} = E \alpha \Delta T\)
Se \(\sigma_{termico} > \sigma_{adm}\), há risco de trincas ou vazamentos.
Convecção Natural
Número de Grashof:
\begin{equation} Gr = \frac{g\beta \Delta T L^3}{\nu} \end{equation}Força e Torque com Efeitos Térmicos
Força no flange:
\begin{equation} \vec{F} = -[(\rho(T) v^2 + p(T))A](\hat{i}+ \hat{j)} \end{equation}Torque térmico:
\begin{equation} \vec{T}_{termico} = \int r \times (\alpha E \Delta T)d \end{equation}Recomendações para Projeto
Para escoamento:
Use CFD para simular distribuição de pressão e turbulência.
Adote um fator de segurança de 20-50 % nas forças calculadas.
Para efeitos térmicos:
Materiais com baixo \(\alpha\) (ex.: aço inox).
Juntas de expansão termicamente isoladas.
Para transientes:
Amortecedores de pressão para golpes de aríete.
Equações-Chave Resumidas:
| Fenômeno | Equação |
|---|---|
| Força no flange | \(\vec{F} = – (\rho v^2 + p) A (\hat{i} + \hat{j})\) |
| Torque | \(\vec{T} =- (\rho v^2 + p) r A \hat{k}\) |
| Perda de pressão | \(\Delta p=f \frac{L}{D} \frac{\rho v^2}{2}\) |
| Dilatação térmica | \(\Delta L = \alpha L \Delta T\) |
| Tensão térmica | \(\sigma = E \alpha \Delta T\) |
Este modelo integrado permite dimensionar sistemas reais com segurança, considerando desde escoamento ideal até efeitos térmicos e estruturais complexos.
