Para dimensionar um coroa (Sprocket) precisamos conhecer os seguintes dados (Usando uma coroa traseira da Teneré 250 como exemplo):
Dados extraídos da coroa teneré 250:
Passo:![]()
Número de dentes:![]()
Diâmetro do rolo da corrente:![]()
Dados teóricos e calculados
Módulo:![]()
Diâmetro circular de referência (diâmetro primitivo):![]()
![]() D_p = (15.875/PI)*40 (Obs: O Autodesk Inventor só aceita “PI” maiúsculo)
D_p = (15.875/PI)*40 (Obs: O Autodesk Inventor só aceita “PI” maiúsculo)
Ver desenho Cad da coroa traseira:
![]() : diâmetro primitivo (circunferência de base)
: diâmetro primitivo (circunferência de base)![]() : número de dentes🌍
: número de dentes🌍![]() : passo da corrente (ae) (Obs: O passo da coroa é igual ao passo da corrente)
: passo da corrente (ae) (Obs: O passo da coroa é igual ao passo da corrente)
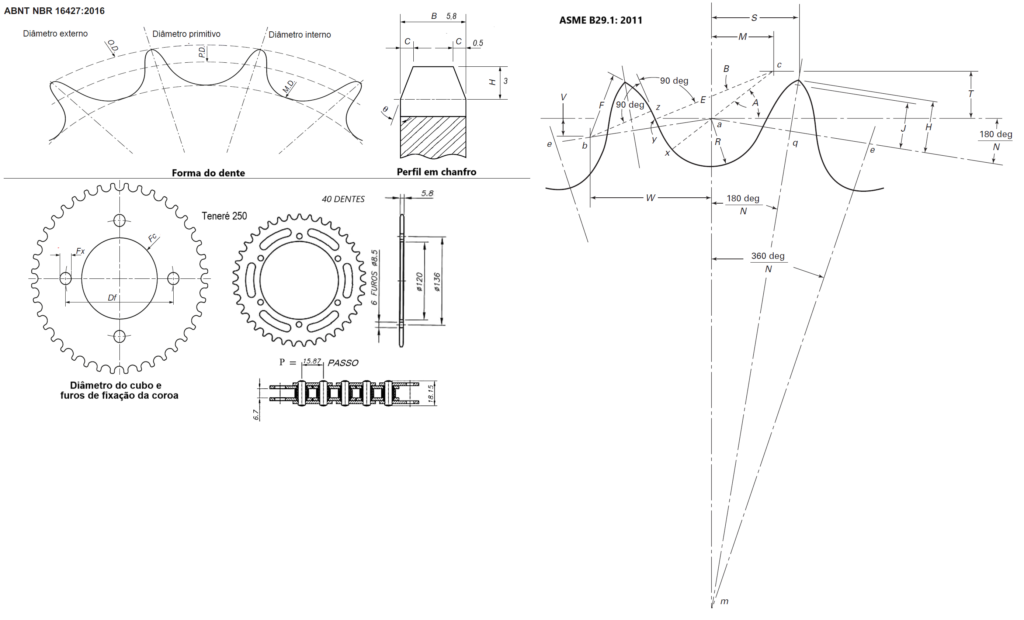
Diâmetro externo aproximado da roda dentada (![]()
![]() J = 0.3*15.875):
J = 0.3*15.875):
![]()
![]() D_e
D_e ![]() 15.875*(0.6 + 1/tan(180/40))
15.875*(0.6 + 1/tan(180/40))
Diâmetro externo da roda dentada quando o dente é pontiagudo:![]()
![]() D_ep = 15.8751/(tan(180/40))+cos(180/40)*((1.005*10.16 + 0.003)-10.16)+2*(sqrt((10.16*(0.8cos(18-56/40)+1.4*cos(17-64/40)-1.3025)-0.0015)^2-(1.4*10.16-15.875/2)^2))
D_ep = 15.8751/(tan(180/40))+cos(180/40)*((1.005*10.16 + 0.003)-10.16)+2*(sqrt((10.16*(0.8cos(18-56/40)+1.4*cos(17-64/40)-1.3025)-0.0015)^2-(1.4*10.16-15.875/2)^2))
Diâmetro da curva de assentamento![]()
![]()
![]() = 1.005*10.16 + 0.003
= 1.005*10.16 + 0.003
Adendo circular:![]() = P*(0.3 – (tan(90/N_a)/2))
= P*(0.3 – (tan(90/N_a)/2))
![]() = Profundidade total do corte com fresa Topping
= Profundidade total do corte com fresa Topping
![]() = D_r/2 + P*(0.3 – tan*(tan(90/N_a)/2))
= D_r/2 + P*(0.3 – tan*(tan(90/N_a)/2))
![]() = Número Intermediário de dentes para faixa de Topping Hob
= Número Intermediário de dentes para faixa de Topping Hob
NOTAS GERAIS:
(a) Os Ângulos são calculados da seguinte forma:![]()
![]() A = 35+60/40
A = 35+60/40![]()
![]() B = 18-56/40
B = 18-56/40
Ângulo de pressão para uma corrente nova:![]()
Ângulo de pressão mínimo:![]()
O ângulo de pressão médio: ![]()
b) Dimensões dimensões são calculadas da seguinte forma:![]()
![]()
![]()
![]() E = 1.3025*10.16+0.0015
E = 1.3025*10.16+0.0015
![]()
![]() F = 10.16*(0.8*cos(18-56/40)+1.4*cos(17-64/40)-1.3025)-0.0015
F = 10.16*(0.8*cos(18-56/40)+1.4*cos(17-64/40)-1.3025)-0.0015
![]()
![]() H = sqrt((10,16*(0,8cos(18-56/19) +1,4*cos(17-64/19)-1,3025)-0,0015)^2-(1,4*10,16- 15,875/2)^2)
H = sqrt((10,16*(0,8cos(18-56/19) +1,4*cos(17-64/19)-1,3025)-0,0015)^2-(1,4*10,16- 15,875/2)^2)
![]()
![]() M = 0.8*10.16*cos(35+60/40)
M = 0.8*10.16*cos(35+60/40)
![]()
![]() R = 0.5025*10.16+0,0015
R = 0.5025*10.16+0,0015
![]()
![]() S = 15.875/2*cos(180/40)+sqrt((10.16*(0.8*cos(18-56/40)+1.4*cos(17-64/40)-1.3025)-0.0015)^2-(1.4*10.16-15.875/2)^2)*sin(180/40)
S = 15.875/2*cos(180/40)+sqrt((10.16*(0.8*cos(18-56/40)+1.4*cos(17-64/40)-1.3025)-0.0015)^2-(1.4*10.16-15.875/2)^2)*sin(180/40)
![]()
![]() T = 0.8*10.16*sin(35+60/40)
T = 0.8*10.16*sin(35+60/40)
![]()
![]() V = 1.4*10.16*sin(180/40)
V = 1.4*10.16*sin(180/40)
![]()
![]() W =
W =![]()
Comprimento do arco da corda:
xy = (2.605 Dr+0.003)sin(9-28/N) ![]() xy = (2.605*10.16+0.003)*sin(9-28/40)
xy = (2.605*10.16+0.003)*sin(9-28/40)
yz = Dr(1.4 sin(17-64/N)-0.8(18-56/N)) ![]() yz=10.16*(1.4*sin(17-64/140)-0.8*sin(18-56/40))
yz=10.16*(1.4*sin(17-64/140)-0.8*sin(18-56/40))
REFERÊNCIAS UTILIZADAS:
ASME B29.1-2011: Precision Power Transmission Roller Chains, Attachments, and Sprockets [Paperback] The American Society of Mechanical Engineers
NBR16427 2016: Correntes, coroas e pinhões de motocicletas, motonetas, ciclomotores, triciclos e quadriciclos – Dimensões e métodos de ensaio
Norton, Robert L. Projeto de máquinas [recurso eletrônico] : uma abordagem integrada / Robert L. Norton – 4. ed. – Porto Alegre : Bookman, 2013.


Deixe um comentário