THOMAS R. KANE![]()
Department of Applied Mechanics, Stanford University, Stanford, California, U.S.A.
Received 16 September 1974
![]() As considerações cinemáticas desempenham um papel importante na análise dinâmica de veículos tipo monociclos. Este artigo aborda questões cinemáticas que devem ser enfrentadas no decorrer de toda análise desse tipo. Um modelo matemático é construído; são desenvolvidas equações aplicáveis quando ambas as rodas estão em contato de rolamento com uma superfície plana de apoio; são analisadas curvas em regime permanente; e os resultados são discutidos em detalhes.
As considerações cinemáticas desempenham um papel importante na análise dinâmica de veículos tipo monociclos. Este artigo aborda questões cinemáticas que devem ser enfrentadas no decorrer de toda análise desse tipo. Um modelo matemático é construído; são desenvolvidas equações aplicáveis quando ambas as rodas estão em contato de rolamento com uma superfície plana de apoio; são analisadas curvas em regime permanente; e os resultados são discutidos em detalhes.
Introdução
Estudos relacionados à dinâmica de veículos de via única surgiram na literatura técnica ao longo dos últimos 75 anos.![]() Durante esse período, o interesse mudou gradualmente em questões relacionadas à estabilidade e às qualidades de manuseio para o tópico da interação entre o condutor e o veículo, um assunto que se tornou passível de exploração detalhada somente com a chegada dos computadores de alta velocidade. Mais precisamente, talvez, pode-se dizer que uma tendência para ampliar o escopo das investigações de modo a incluir a consideração da interação condutor-veículo começou a se manifestar, embora a estabilidade e a qualidade do manuseio tenham continuado a receber atenção; a referência (6) é um caso recente em questão.
Durante esse período, o interesse mudou gradualmente em questões relacionadas à estabilidade e às qualidades de manuseio para o tópico da interação entre o condutor e o veículo, um assunto que se tornou passível de exploração detalhada somente com a chegada dos computadores de alta velocidade. Mais precisamente, talvez, pode-se dizer que uma tendência para ampliar o escopo das investigações de modo a incluir a consideração da interação condutor-veículo começou a se manifestar, embora a estabilidade e a qualidade do manuseio tenham continuado a receber atenção; a referência (6) é um caso recente em questão.
O uso cada vez mais extensivo de computadores tem sido acompanhado por outra mudança nas análises de veículos de pista única: os modelos matemáticos contidos a essas análises têm se tornado cada vez mais elaborados. Agora, isso pode significar que o trabalho de autores modernos levou a informações de maior valor do que aquelas obtidas por seus antecessores. Mas esse não é necessariamente o caso, pois existe a possibilidade de que tanto se perca hoje em dia por meio das dificuldades de interpretação associadas a uma formulação excessivamente complexa, ou por causa das imprecisões numéricas resultantes disso, quanto se perdeu antes por meio de simplificação excessiva. Idealmente, portanto, deveríamos buscar formular os problemas de uma forma que permita explorar o potencial da computação de alta velocidade sem sacrificar desnecessariamente a compreensão do problema. Em outras palavras, a formulação do problema é tão importante hoje quanto era no passado. O presente artigo tem como objetivo facilitar essa tarefa.
Considerações cinemáticas estão entre os principais fatores que complicam análises de veículos de via única, pois há uma série de questões bastante sutis que devem ser respondidas, explícita ou implicitamente, no curso da realização de tais análises. Entre elas estão as seguintes: Qual do ponto da roda está em contato com o solo quando o ângulo de direção (![]() ) e o ângulo de rolagem (
) e o ângulo de rolagem (![]() ) diferem de zero? Como a taxa de inclinação (
) diferem de zero? Como a taxa de inclinação (![]() ) é afetada pela taxa de rolagem e pela taxa de direção? Como as taxas de rotação das rodas estão relacionadas entre si? Quantos graus de liberdade um veículo de via única possui? Essas perguntas são respondidas explicitamente na sequência para um veículo que possui duas rodas, cada uma modelada como um toro rígido que rola sem escorregar em um suporte plano.
) é afetada pela taxa de rolagem e pela taxa de direção? Como as taxas de rotação das rodas estão relacionadas entre si? Quantos graus de liberdade um veículo de via única possui? Essas perguntas são respondidas explicitamente na sequência para um veículo que possui duas rodas, cada uma modelada como um toro rígido que rola sem escorregar em um suporte plano.
(A razão para considerar um toro, em vez de um disco fino, como tem sido feito pela maioria de outros autores, é que o raio do círculo gerador do toro é uma parte apreciável do raio da roda no caso de scooters. Além disso, a inclusão deste efeito não complica indevidamente as coisas.)
O artigo é organizado da seguinte forma: a seção ![]() contém uma descrição do veículo e as definições dos símbolos usados na análise que se segue. Na seção
contém uma descrição do veículo e as definições dos símbolos usados na análise que se segue. Na seção ![]() , cinco relações associadas ao fato de que ambas as rodas devem estar em contato com a superfície de suporte são derivadas. Cinco outras equações fundamentais são desenvolvidas na seção
, cinco relações associadas ao fato de que ambas as rodas devem estar em contato com a superfície de suporte são derivadas. Cinco outras equações fundamentais são desenvolvidas na seção ![]() , levando em consideração o rolamento sem deslizamento. A seção
, levando em consideração o rolamento sem deslizamento. A seção ![]() trata brevemente da curva estável. Finalmente, uma discussão abrangente dos resultados é apresentada na seção
trata brevemente da curva estável. Finalmente, uma discussão abrangente dos resultados é apresentada na seção ![]() .
.
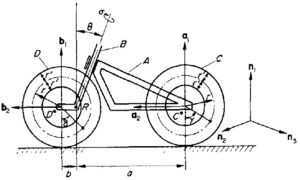
Descrição do veículo
A Fig.1 é uma representação esquemática de um veículo de via única que consiste em um chassi ![]() , garfo
, garfo ![]() , roda traseira
, roda traseira ![]() e roda dianteira
e roda dianteira ![]() . O veículo é descrito geometricamente pelas constantes
. O veículo é descrito geometricamente pelas constantes ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() .
.
A “configuração” do veículo é caracterizada pelo ângulo de caster (![]() )
) ![]() entre os planos centrais de
entre os planos centrais de ![]() e
e ![]() , e pelos ângulos de rotação das rodas
, e pelos ângulos de rotação das rodas ![]() e
e ![]() . Para a configuração representada na Fig.1,
. Para a configuração representada na Fig.1, ![]() é igual a zero enquanto
é igual a zero enquanto ![]() e
e ![]() são positivos.
são positivos.
A orientação de ![]() em um referencial “fixo”
em um referencial “fixo” ![]() depende de três ângulos gerados da seguinte forma: Sejam
depende de três ângulos gerados da seguinte forma: Sejam ![]() ,
, ![]() e
e ![]() um conjunto de vetores unitários ortonormais fixos em
um conjunto de vetores unitários ortonormais fixos em ![]() , conforme mostrado na Fig.1, e sejam
, conforme mostrado na Fig.1, e sejam ![]() ,
, ![]() e
e ![]() um conjunto semelhante de vetores unitários fixos em
um conjunto semelhante de vetores unitários fixos em ![]() , com
, com ![]() normal ao plano que suporta o veículo.
normal ao plano que suporta o veículo.
Em seguida, alinhe ![]() com
com ![]() (
(![]() ) e então sujeite
) e então sujeite ![]() sucessivamente a uma rotação
sucessivamente a uma rotação ![]() de quantidade
de quantidade ![]() , uma rotação
, uma rotação ![]() de quantidade
de quantidade ![]() , e uma rotação
, e uma rotação ![]() de quantidade
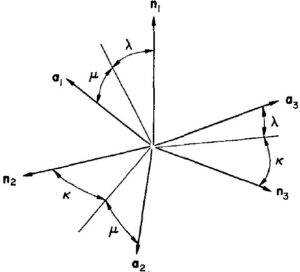
de quantidade ![]() realizando cada uma dessas rotações no sentido destro em torno de um eixo paralelo ao vetor unitário sob consideração em sua orientação atual. Os três ângulos são chamados de ângulo de guinada (
realizando cada uma dessas rotações no sentido destro em torno de um eixo paralelo ao vetor unitário sob consideração em sua orientação atual. Os três ângulos são chamados de ângulo de guinada (![]() ), ângulo de rolagem (
), ângulo de rolagem (![]() ) e ângulo de inclinação (
) e ângulo de inclinação (![]() ). Eles são mostrados na Fig.2, com
). Eles são mostrados na Fig.2, com ![]() ,
, ![]() e
e ![]() em suas respectivas posições finais.
em suas respectivas posições finais.
 ), rotação (
), rotação ( ) e inclinação (
) e inclinação (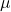 ).
).Na sequência, será conveniente empregar três constantes além das já mencionadas. Estas são ![]() ,
, ![]() e
e ![]() , definidas como
, definidas como ![]()
(1) 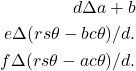
Restrições de contato
Se ![]() e
e ![]() designam respectivamente os pontos de
designam respectivamente os pontos de ![]() e
e ![]() que estão em contato com o plano de suporte quando
que estão em contato com o plano de suporte quando ![]() ,
, ![]() ,
, ![]() e
e ![]() têm valores gerais, então a localização de
têm valores gerais, então a localização de ![]() em relação a
em relação a ![]() e a de
e a de ![]() em relação a
em relação a ![]() podem ser descritas em termos de dois ângulos.
podem ser descritas em termos de dois ângulos.
![]() s
s![]() e c
e c![]() são abreviações para sin
são abreviações para sin![]() e cos
e cos![]() , respectivamente. Similarmente para s
, respectivamente. Similarmente para s![]() , c
, c![]() , etc.
, etc.
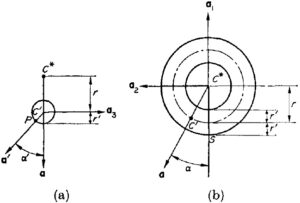
Para ![]() , estes são
, estes são ![]() e
e ![]() , definidos como segue: Um plano que é normal ao plano central de
, definidos como segue: Um plano que é normal ao plano central de ![]() e contém tanto
e contém tanto ![]() quanto o centro
quanto o centro ![]() de
de ![]() intercepta a superfície toroidal do pneu em um círculo centrado em um ponto
intercepta a superfície toroidal do pneu em um círculo centrado em um ponto ![]() e tendo um raio
e tendo um raio ![]() , como mostrado na Fig.3(a).
, como mostrado na Fig.3(a). ![]() é mostrado novamente na Fig.3(b); e o ponto
é mostrado novamente na Fig.3(b); e o ponto ![]() neste esboço está na linha que passa por
neste esboço está na linha que passa por ![]() e é paralela a
e é paralela a ![]() .
. ![]() é o ângulo entre as linhas
é o ângulo entre as linhas ![]() e
e ![]() , e
, e ![]() é o ângulo entre a extensão da linha
é o ângulo entre a extensão da linha ![]() e a linha
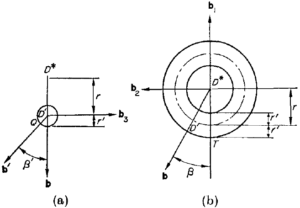
e a linha ![]() . Para
. Para ![]() , os ângulos correspondentes são
, os ângulos correspondentes são ![]() e
e ![]() , como mostrado na Fig.4.
, como mostrado na Fig.4.
Os ângulos ![]() ,
, ![]() ,
, ![]() ,
, ![]() , bem como o ângulo de inclinação
, bem como o ângulo de inclinação ![]() dependem do ângulo de direção
dependem do ângulo de direção ![]() e do ângulo de rolagem
e do ângulo de rolagem ![]() . Para explorar essa dependência, pode-se introduzir vetores unitários
. Para explorar essa dependência, pode-se introduzir vetores unitários ![]() e
e ![]() como mostrado na Fig.3, e vetores unitários correspondentes
como mostrado na Fig.3, e vetores unitários correspondentes ![]() e
e ![]() como na Fig.4, e usá-los para investigar as consequências dos seguintes fatos: No ponto
como na Fig.4, e usá-los para investigar as consequências dos seguintes fatos: No ponto ![]() , a normal à superfície do pneu deve ser paralela a
, a normal à superfície do pneu deve ser paralela a ![]() ; similarmente, no ponto
; similarmente, no ponto ![]() . Portanto
. Portanto
(2) ![]()
O vetor que une ![]() a
a ![]() deve ser perpendicular a
deve ser perpendicular a ![]() , o que significa que (ver Figs. ??, ?? e ??)
, o que significa que (ver Figs. ??, ?? e ??)
(3) ![]()
ou, em vista da equação (2),
(4) ![]()
Agora, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() podem ser expressos em termos de
podem ser expressos em termos de ![]()
![]() ,
, ![]() ; e as equações (2) e (4) podem ser expressas como as sete equações escalares
; e as equações (2) e (4) podem ser expressas como as sete equações escalares
(5) 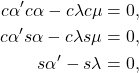
(6) ![]()
(7) ![]()
(8) ![]()
e
(9) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} \{(b + rs\beta) s\theta c\theta(c\sigma - 1) + r c\alpha \\ - rc\beta[c\sigma + c^2 \theta(1 - c\sigma)\} c\lambda c\mu \\ - \{a + (b + r s\beta)[c\sigma + s^2 \theta(1 - c\sigma)] \\ - r s\alpha + r c\beta s\theta c\theta (1 - c\sigma)\} c\lambda s\mu \\ + [r c\beta s\theta - (b + r s\beta) c\theta] s\sigma s\lambda = 0. \end{aligned} \end{eqnarray*}](https://alvesintech.com/wp-content/ql-cache/quicklatex.com-fc2a2fa11dbe7b0390d1b5822524b573_l3.png)
Resolver essas equações explicitamente e exatamente para ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() como funções de
como funções de ![]() e
e ![]() parece ser impossível. No entanto, uma solução aproximada fisicamente significativa pode ser obtida pelo raciocínio da seguinte forma: quando
parece ser impossível. No entanto, uma solução aproximada fisicamente significativa pode ser obtida pelo raciocínio da seguinte forma: quando ![]() , todas as equações (5) – (9) são satisfeitas (para todos os
, todas as equações (5) – (9) são satisfeitas (para todos os ![]() ) se
) se
(10) ![]()
Portanto, se ![]() e
e ![]() são expressos como
são expressos como
(11) ![]()
\noindent então, quando ![]() é tão pequeno que todas as potências de a acima do primeiro são desprezíveis, as equações (5) – (8) podem ser substituídas por um sistema linear em
é tão pequeno que todas as potências de a acima do primeiro são desprezíveis, as equações (5) – (8) podem ser substituídas por um sistema linear em ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() , a saber
, a saber
(12) ![]()
(13) ![]()
\noindent enquanto a equação (9) reduz com o auxílio das equações (1) para
(14) ![]()
Resolvendo essas equações para ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() e usando as equações (11), chega-se a
e usando as equações (11), chega-se a
(15) ![]()
(16) ![]()
(17) ![]()
Restrições de rolamento
Se ambas as rodas rolam sem deslizar em um plano fixo em ![]() , isto é, se tanto
, isto é, se tanto ![]() quanto
quanto ![]() têm velocidade zero em
têm velocidade zero em ![]() , então as taxas de tempo de mudança dos ângulos de rotação da roda (
, então as taxas de tempo de mudança dos ângulos de rotação da roda (![]() ,
,![]() ), o ângulo de direção (
), o ângulo de direção (![]() ), o ângulo de rolagem (
), o ângulo de rolagem (![]() ) e o ângulo de guinada (
) e o ângulo de guinada (![]() ) não são independentes entre si. De fato,
) não são independentes entre si. De fato, ![]() e
e ![]() podem ser considerados funções de
podem ser considerados funções de ![]() ,
, ![]() e
e ![]() , como será mostrado agora.
, como será mostrado agora.
As velocidades dos centros ![]() e
e ![]() de
de ![]() e
e ![]() podem ser expressas como
podem ser expressas como
(18) 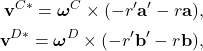
\noindent onde ![]() e
e ![]() são, respectivamente, as velocidades angulares de
são, respectivamente, as velocidades angulares de ![]() e
e ![]() em
em ![]() ; e a velocidade do ponto
; e a velocidade do ponto ![]() (ver Fig. ??), um ponto fixo tanto em
(ver Fig. ??), um ponto fixo tanto em ![]() quanto em
quanto em ![]() , é dada tanto por
, é dada tanto por ![]() ) quanto por
) quanto por ![]() . Igualando essas duas expressões e usando as equações (18), obtém-se
. Igualando essas duas expressões e usando as equações (18), obtém-se
(19) 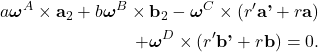
Para formular equações escalares adequadas correspondentes a esta equação vetorial, é conveniente primeiro observar que
(20) ![]()
(21) ![]()
(22) ![]()
\noindent para que a equação (19) possa ser reescrita como (lembre-se de que ![]() )
)
(23) 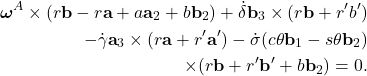
Próximo,
(24) 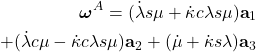
\noindent ou, após a eliminação de ![]() pelo uso da equação (17) e subsequente linearização em
pelo uso da equação (17) e subsequente linearização em ![]() ,
,
(25) 
As multiplicações cruzadas indicadas na equação (23) podem agora ser realizadas após se ter expressado todos os vetores unitários em termos de ![]() ,
, ![]() ,
, ![]() . Usando as equações (15) e (16), e linearizando novamente em
. Usando as equações (15) e (16), e linearizando novamente em ![]() , descobre-se então com o auxílio das equações (1) que a suposição de rolar sem deslizar leva às três equações seguintes:
, descobre-se então com o auxílio das equações (1) que a suposição de rolar sem deslizar leva às três equações seguintes:
(26) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} \dot{\kappa}(d + r c\theta \sigma tan \lambda) s\lambda \\ + (\dot{\lambda} de \sigma tan \lambda + \dot{\sigma}de + \dot{\delta}rf\sigma - \dot{\gamma}re\sigma) tan \lambda \\ + r'[(\dot{\delta}f - \dot{\gamma}e)\sigma + \dot{\sigma} s\theta] s\lambda = 0, \end{aligned} \end{eqnarray*}](https://alvesintech.com/wp-content/ql-cache/quicklatex.com-ebae8051b4318576e5a72e0374d78862_l3.png)
(27) 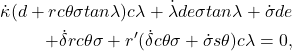
(28) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} \dot{\kappa}de\sigma c\lambda + r(\dot{\delta} - \dot{\gamma}) \\ + r'[\dot{\delta}(c\lambda - \sigma s\theta s\lambda) - \dot{\gamma} c\lambda + \dot{\sigma} c\theta \lambda] = 0. \end{aligned} \end{eqnarray*}](https://alvesintech.com/wp-content/ql-cache/quicklatex.com-feb28fd916d0e74065fd64efe62a54cb_l3.png)
Existem agora duas possibilidades: ![]() , caso em que a equação (26) é satisfeita de forma idêntica, enquanto as equações (27) e (28) tornam-se, respectivamente,
, caso em que a equação (26) é satisfeita de forma idêntica, enquanto as equações (27) e (28) tornam-se, respectivamente,
(29) ![]()
(30) ![]()
Resolvendo a equação (30) para ![]() , substituindo o resultado na equação (29) e linearizando em
, substituindo o resultado na equação (29) e linearizando em ![]() , chega-se a uma expressão para
, chega-se a uma expressão para ![]() , e a equação (30) pode então ser usada para encontrar
, e a equação (30) pode então ser usada para encontrar ![]() :
:
(31) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} \dot{\delta} = \dot{\gamma},\\ \dot{\kappa} = - [\dot{\sigma}(e + r' s\theta d^{-1}) + \sigma\dot{\gamma}(r + r')c\theta d^{-1}]. \end{aligned} \end{eqnarray*}](https://alvesintech.com/wp-content/ql-cache/quicklatex.com-5595e3f52600dfaebf8f06e198461838_l3.png)
Alternativamente, se ![]() , a divisão da equação (26) por
, a divisão da equação (26) por ![]() é permitida e produz
é permitida e produz
(32) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} \dot{\kappa}(d + r c\theta \sigma tan \lambda) c\lambda + \dot{\lambda}de \sigma tan \lambda \\ + \dot{\sigma}de + \dot{\delta}rf\sigma - \dot{\gamma}re\sigma \\ + r'[(\dot{\delta}f - \dot{\gamma}e)\sigma + \dot{\sigma} s\theta]c\lambda = 0. \end{aligned} \end{eqnarray*}](https://alvesintech.com/wp-content/ql-cache/quicklatex.com-9f8c410d982668b904999d64d3c30c93_l3.png)
Agora, segue-se da multiplicação da equação (28) com ![]() que
que ![]() ; e, quando
; e, quando ![]() é eliminado da equação (32) por meio desta substituição, e é notado que
é eliminado da equação (32) por meio desta substituição, e é notado que ![]() em virtude das equações (1), parece que a equação (32) é, de fato, equivalente à equação (27). Assim, o requisito de que não haja deslizamento em
em virtude das equações (1), parece que a equação (32) é, de fato, equivalente à equação (27). Assim, o requisito de que não haja deslizamento em ![]() e
e ![]() é visto como satisfeito sempre que as equações (27) e (28) sejam satisfeitas; e a solução dessas equações produz (após linearização em
é visto como satisfeito sempre que as equações (27) e (28) sejam satisfeitas; e a solução dessas equações produz (após linearização em ![]() )
)
(33) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} \dot{\delta} = \dot{\gamma}[1 + \sigma r' s\lambda(r + r' c\lambda)^{-1} s\theta] \\ - \dot{\sigma} r' s\lambda(r + r' c\lambda)^{-1} c\theta, \end{aligned} \end{eqnarray*}](https://alvesintech.com/wp-content/ql-cache/quicklatex.com-a947480f731740a43d4e6e4321b9f2f8_l3.png)
(34) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} \dot{\kappa} = [\dot{\lambda}\sigma e tan\lambda + \dot{\sigma}(e + r' c\lambda s\theta d^{-1}) \\ + \dot{\gamma}\sigma(r + r' c\lambda) c\theta d^{-1}]sec \lambda. \end{aligned} \end{eqnarray*}](https://alvesintech.com/wp-content/ql-cache/quicklatex.com-147be50c1976cdebd1a3a2112430ed68_l3.png)
Estes resultados, embora tenham sido obtidos sujeitos à exigência de que ![]() seja diferente de zero, são válidos também quando
seja diferente de zero, são válidos também quando ![]() desaparece, pois reduzem-se às equações (31) quando
desaparece, pois reduzem-se às equações (31) quando ![]() é igualado a zero.
é igualado a zero.
Até o momento, nenhuma menção foi feita à localização de qualquer ponto do veículo em relação ao referencial ![]() . Ou seja, nenhuma coordenada de posição foi introduzida. Este tópico foi adiado para enfatizar o fato de que todos os desenvolvimentos anteriores são totalmente independentes desta questão.
. Ou seja, nenhuma coordenada de posição foi introduzida. Este tópico foi adiado para enfatizar o fato de que todos os desenvolvimentos anteriores são totalmente independentes desta questão.
Se ![]() é um ponto fixo no referencial
é um ponto fixo no referencial ![]() , o vetor posição de
, o vetor posição de ![]() em relação a
em relação a ![]() e a velocidade de
e a velocidade de ![]() podem ser expressos, respectivamente, como
podem ser expressos, respectivamente, como
(35) ![]()
Entretanto, ![]() também é dado pela primeira das equações (18). Igualando as duas expressões para
também é dado pela primeira das equações (18). Igualando as duas expressões para ![]() , referindo-se às equações (21) e (24), usando a equação (34) para eliminar
, referindo-se às equações (21) e (24), usando a equação (34) para eliminar ![]() , e expressando todos os vetores em termos de
, e expressando todos os vetores em termos de ![]() ,
, ![]() ,
, ![]() , obtém-se (após uma quantidade considerável de álgebra) as seguintes equações diferenciais:
, obtém-se (após uma quantidade considerável de álgebra) as seguintes equações diferenciais:
(36) ![]()
(37) ![]()
(38) ![]()
Giro estável
Diz-se que o veículo está em uma curva estável quando está se movendo de tal forma que o ângulo de direção ![]() , o ângulo de rolagem
, o ângulo de rolagem ![]() e a taxa de rotação da roda traseira
e a taxa de rotação da roda traseira ![]() têm valores constantes, digamos
têm valores constantes, digamos ![]() ,
, ![]() e
e ![]() . Nessas circunstâncias, segue das equações (17), (33) e (34) que
. Nessas circunstâncias, segue das equações (17), (33) e (34) que ![]() ,
, ![]() e
e ![]() também têm valores constantes, digamos
também têm valores constantes, digamos ![]() ,
, ![]() e
e ![]() , com
, com
(39) ![]()
Além disso, o centro ![]() de
de ![]() move-se num círculo cujo raio
move-se num círculo cujo raio ![]() pode ser encontrado aproveitando o fato de que a velocidade de
pode ser encontrado aproveitando o fato de que a velocidade de ![]() é agora dada tanto por
é agora dada tanto por ![]() , onde
, onde ![]() é um vetor unitário tangente ao círculo, quanto pelo membro direito da segunda das equações (35), de modo que, em vista das equações (36) – (39),
é um vetor unitário tangente ao círculo, quanto pelo membro direito da segunda das equações (35), de modo que, em vista das equações (36) – (39),
(40) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \begin{aligned} -\rho \hat{\dot{\gamma}}\hat{\sigma}(r + r' c\hat{\lambda})d^{-1} c\theta sec \hat{\lambda}\boldsymbol{\tau} \\ = \hat{\dot{\gamma}}[r + r' c\hat{\lambda} - \hat{\sigma} tan \hat{\lambda}rd^{-1}(r + r' c\lambda) c\theta] \\ \times (c\kappa \textbf{n}_2 + s\kappa \textbf{n}_3). \end{aligned} \end{eqnarray*}](https://alvesintech.com/wp-content/ql-cache/quicklatex.com-014976b4930677252afbca98e4deb6bc_l3.png)
Igualando as magnitudes dos vetores nos membros esquerdo e direito desta equação, chega-se a
(41) ![]()
Discurssão
Os principais resultados analíticos obtidos nas seções anteriores são as equações (15) – (17), (33), (34), (36) – (39) e (41). Todas elas são aproximadas por natureza, pois sua derivação envolveu o requisito de que ![]() seja pequeno. No entanto, essa restrição não prejudica sua utilidade significativamente, pois (como será mostrado mais tarde) até mesmo curvas bastante fechadas podem ser executadas com um ângulo bem pequeno, digamos menor que 15°, desde que
seja pequeno. No entanto, essa restrição não prejudica sua utilidade significativamente, pois (como será mostrado mais tarde) até mesmo curvas bastante fechadas podem ser executadas com um ângulo bem pequeno, digamos menor que 15°, desde que ![]() seja irrestrito; e nenhuma restrição foi colocada em
seja irrestrito; e nenhuma restrição foi colocada em ![]() . Os benefícios derivados da exigência de que
. Os benefícios derivados da exigência de que ![]() seja pequeno são, é claro, notáveis: o caráter explícito e a relativa simplicidade das equações citadas são consequências diretas da linearização em
seja pequeno são, é claro, notáveis: o caráter explícito e a relativa simplicidade das equações citadas são consequências diretas da linearização em ![]() . Além disso, essas equações serviriam a um propósito útil mesmo no caso improvável de que se exigissem resultados mais exatos, pois seria possível usá-las para realizar uma solução iterativa das equações (5) – (9) e versões não linearizadas das equações (26) – (28).
. Além disso, essas equações serviriam a um propósito útil mesmo no caso improvável de que se exigissem resultados mais exatos, pois seria possível usá-las para realizar uma solução iterativa das equações (5) – (9) e versões não linearizadas das equações (26) – (28).
As equações (15) – (17) mostram que, em geral, os pontos de contato ![]() e
e ![]() (ver Figuras Fig.3 e Fig.4) deslocam-se respectivamente em relação ao chassi
(ver Figuras Fig.3 e Fig.4) deslocam-se respectivamente em relação ao chassi ![]() e ao garfo
e ao garfo ![]() , e o ângulo de passo
, e o ângulo de passo ![]() muda, sempre que ocorre uma alteração no ângulo de direção
muda, sempre que ocorre uma alteração no ângulo de direção ![]() ou no ângulo de rolagem
ou no ângulo de rolagem ![]() . Esta regra tem uma exceção no que diz respeito ao ângulo de passo: uma vez que
. Esta regra tem uma exceção no que diz respeito ao ângulo de passo: uma vez que ![]() (ver equações (1)) pode ser feito desaparecer escolhendo
(ver equações (1)) pode ser feito desaparecer escolhendo ![]() ,
, ![]() e
e ![]() tais que
tais que ![]() , é possível fazer
, é possível fazer ![]() igual a zero para \textit{todos}
igual a zero para \textit{todos} ![]() e
e ![]() . Este fato pode ser reafirmado de uma forma interessante trazendo uma quantidade chamada “trail” para a discussão, esta quantidade sendo definida como a distância
. Este fato pode ser reafirmado de uma forma interessante trazendo uma quantidade chamada “trail” para a discussão, esta quantidade sendo definida como a distância ![]() entre os pontos
entre os pontos ![]() e
e ![]() na Fig.5, onde
na Fig.5, onde ![]() é o ponto de contato da roda dianteira com o plano de apoio quando
é o ponto de contato da roda dianteira com o plano de apoio quando ![]() , e
, e ![]() é o ponto de intersecção deste plano e do eixo de rotação do garfo
é o ponto de intersecção deste plano e do eixo de rotação do garfo ![]() . Assim,
. Assim,
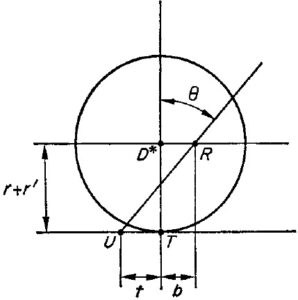
(42) ![]()
\noindent e, resolvendo para ![]() e substituindo na segunda das equações (1), pode-se expressar
e substituindo na segunda das equações (1), pode-se expressar ![]() como
como
(43) ![]()
Consequentemente, ![]() desaparece para todos os
desaparece para todos os ![]() e
e ![]() se t tem um valor
se t tem um valor ![]() dado por
dado por
(44) ![]()
A quantidade ![]() tem um efeito direto também na taxa de guinada
tem um efeito direto também na taxa de guinada ![]() , como pode ser visto na equação (34). Se
, como pode ser visto na equação (34). Se ![]() ,
, ![]() não é afetado pela taxa de rolagem
não é afetado pela taxa de rolagem ![]() . A importância relativa desse efeito cresce à medida que a velocidade do veículo diminui
. A importância relativa desse efeito cresce à medida que a velocidade do veículo diminui ![]() , ou seja, quando a taxa de rotação da roda traseira
, ou seja, quando a taxa de rotação da roda traseira ![]() se torna pequena.
se torna pequena.
Em grande parte do trabalho sobre o assunto de veículos de via única, assume-se que as taxas de rotação das rodas traseiras e dianteiras, ![]() e
e ![]() , são iguais entre si. A equação (33) mostra que isso ocorre apenas em circunstâncias especiais, por exemplo, quando
, são iguais entre si. A equação (33) mostra que isso ocorre apenas em circunstâncias especiais, por exemplo, quando ![]() e
e ![]() desaparecem ou quando
desaparecem ou quando ![]() . De fato, parece que qualquer uma dessas taxas pode diferir de zero, enquanto a outra é igual a zero. Vale a pena notar que essas conclusões não teriam sido alcançadas se cada roda tivesse sido modelada como um disco fino, em vez de um toro, ou seja, se
. De fato, parece que qualquer uma dessas taxas pode diferir de zero, enquanto a outra é igual a zero. Vale a pena notar que essas conclusões não teriam sido alcançadas se cada roda tivesse sido modelada como um disco fino, em vez de um toro, ou seja, se ![]() tivesse sido deixado de fora.
tivesse sido deixado de fora.
A possibilidade de executar uma curva estável de raio relativamente pequeno usando um pequeno ângulo de direção pode ser estabelecida por referência à equação (41). Por exemplo, suponha que ![]() pol.,
pol., ![]() pol. e
pol. e ![]() °, sendo estes valores representativos para uma bicicleta. Então, um ângulo de direção de
°, sendo estes valores representativos para uma bicicleta. Então, um ângulo de direção de ![]() ° combinado com um ângulo de rolagem de
° combinado com um ângulo de rolagem de ![]() ° produz um raio de curva de cerca de
° produz um raio de curva de cerca de ![]() ft, e isso pode ser reduzido para apenas
ft, e isso pode ser reduzido para apenas ![]() ft aumentando o ângulo de direção para o modesto valor de
ft aumentando o ângulo de direção para o modesto valor de ![]() °. Além disso, se o ângulo de rolagem for aumentado para
°. Além disso, se o ângulo de rolagem for aumentado para ![]() °, que é um valor grande, mas não irreal, um raio de curva de
°, que é um valor grande, mas não irreal, um raio de curva de ![]() ft é obtido com o mesmo ângulo de direção. Como para
ft é obtido com o mesmo ângulo de direção. Como para ![]() ° o erro na substituição de
° o erro na substituição de ![]() por
por ![]() é de apenas cerca de
é de apenas cerca de ![]() por cento de
por cento de ![]() , a presente teoria parece ser inteiramente adequada para fins práticos.
, a presente teoria parece ser inteiramente adequada para fins práticos.
Ainda sobre o assunto de curvas estáveis, vale a pena notar que todas as afirmações feitas até agora são válidas independentemente da velocidade do veículo. Isso não quer dizer, no entanto, que a satisfação da equação (41) garanta a possibilidade de executar uma curva estável sob consideração a uma velocidade pré-atribuída. Em outras palavras, a equação (41) é uma condição necessária, mas não suficiente, para uma curva estável. Certas condições decorrentes de considerações dinâmicas devem ser satisfeitas além da equação (41) se uma dada curva estável for fisicamente possível.
Embora apenas tópicos puramente cinemáticos tenham sido discutidos até agora, os resultados obtidos podem ser especialmente úteis em conexão com análises dinâmicas. Por exemplo, se equações de movimento devem ser escritas apelando para um princípio de Lagrange, que frequentemente é uma opção atraente porque facilita a eliminação de forças de restrição, então coordenadas generalizadas devem ser designadas e uma determinação do número de graus de liberdade deve ser feita. Essas são questões que não podem ser resolvidas de uma vez por todas, pois sua disposição depende dos objetivos da análise em questão. No entanto, considerações semelhantes se aplicam a todos os casos. Por exemplo, suponha que fosse desejado estudar movimentos que podem ocorrer quando a roda traseira é feita para girar em relação a ![]() com uma velocidade angular prescrita como uma função do tempo enquanto um torque, também prescrito como uma função do tempo, é aplicado ao garfo
com uma velocidade angular prescrita como uma função do tempo enquanto um torque, também prescrito como uma função do tempo, é aplicado ao garfo ![]() por um piloto presumivelmente imóvel em relação a
por um piloto presumivelmente imóvel em relação a ![]() .
.
Em termos de símbolos usados anteriormente, o problema seria descobrir a dependência temporal ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Isso não significa, no entanto, que todas essas oito variáveis devem ser tratadas como coordenadas generalizadas, pois
. Isso não significa, no entanto, que todas essas oito variáveis devem ser tratadas como coordenadas generalizadas, pois ![]() pode ser eliminado usando a equação (17), e a equação (36) é facilmente integrável, produzindo
pode ser eliminado usando a equação (17), e a equação (36) é facilmente integrável, produzindo
(45) ![]()
![]() onde
onde ![]() e
e ![]() são os valores das respectivas variáveis sem um instante particular. As seis variáveis que permanecem após
são os valores das respectivas variáveis sem um instante particular. As seis variáveis que permanecem após ![]() e
e ![]() terem sido eliminadas podem ser consideradas coordenadas generalizadas, mas como quatro equações diferenciais de restrição não integráveis ainda precisam ser levadas em conta, a saber, equações (33), (34), (37) e (38), apenas duas equações dinâmicas de movimento precisam ser escritas se uma formulação aplicável a sistemas não holonômicos
terem sido eliminadas podem ser consideradas coordenadas generalizadas, mas como quatro equações diferenciais de restrição não integráveis ainda precisam ser levadas em conta, a saber, equações (33), (34), (37) e (38), apenas duas equações dinâmicas de movimento precisam ser escritas se uma formulação aplicável a sistemas não holonômicos![]() for empregada. Em resumo, pode-se proceder da seguinte forma. Após eliminar
for empregada. Em resumo, pode-se proceder da seguinte forma. Após eliminar ![]() e
e ![]() por referência às equações (17) e (45), escreva equações de movimento de Lagrange (aplicáveis a um sistema não holonômico) para as coordenadas generalizadas
por referência às equações (17) e (45), escreva equações de movimento de Lagrange (aplicáveis a um sistema não holonômico) para as coordenadas generalizadas ![]() e
e ![]() , e integre-as simultaneamente com as equações (33), (34), (37) e (38).
, e integre-as simultaneamente com as equações (33), (34), (37) e (38).
Pode-se dizer que o exemplo recém citado está no meio do caminho entre os extremos que se pode esperar encontrar. Ou seja, uma vez que as equações (17), (33), (34) e (36) – (38) devem ser satisfeitas em todos os casos, nunca é necessário escrever mais do que três equações dinâmicas de movimento, e pode ser suficiente escrever apenas uma.
Finalmente, pode valer a pena mencionar que o fato de um motociclista ter entrado na discussão anterior apenas perifericamente não tem implicações negativas quanto à relevância dos resultados apresentados para análises envolvendo interações complicadas entre motociclista e veículo. Pelo contrário, esses resultados afetam diretamente cada uma dessas análises e, portanto, devem ser levados em consideração.
NOTAÇÕES
![]() – chassi
– chassi
![]() – garfo
– garfo
![]() – roda traseira
– roda traseira
![]() – roda dianteira
– roda dianteira
![]() – dimensão de quadro
– dimensão de quadro
![]() – dimensão do garfo
– dimensão do garfo
![]() – raio da linha central do pneu
– raio da linha central do pneu
![]() & raio da seção transversal do pneu
& raio da seção transversal do pneu
![]() – ângulo de caster (
– ângulo de caster (![]() )
)
![]() – ângulo de direção (
– ângulo de direção (![]() )
)
![]() – ângulo de rotação da roda traseira
– ângulo de rotação da roda traseira
![]() – ângulo de rotação da roda dianteira
– ângulo de rotação da roda dianteira
![]() ,
, ![]() ,
, ![]() – vetores unitários fixos em
– vetores unitários fixos em ![]()
![]() ,
, ![]() ,
, ![]() – vetores unitários fixos em
– vetores unitários fixos em ![]()
![]() ,
, ![]() ,
, ![]() – vetores unitários fixos em
– vetores unitários fixos em ![]()
![]() – ângulo de rotação
– ângulo de rotação
![]() – ângulo de giro
– ângulo de giro
![]() – ângulo de inclinação
– ângulo de inclinação
![]() – distância entre eixos
– distância entre eixos
![]() – parâmetro fork
– parâmetro fork
![]() – parâmetro do chassi
– parâmetro do chassi
![]() – pontos de contato da roda
– pontos de contato da roda
![]() : – ponto fixo em
: – ponto fixo em ![]() e
e ![]()
![]() – coordenadas angulares de
– coordenadas angulares de ![]()
![]() – coordenadas angulares de
– coordenadas angulares de ![]()
![]() – centros de
– centros de ![]() ,
, ![]()
![]() ,
, ![]() – pontos em
– pontos em ![]() ,
, ![]()
![]() – vetores unitários usados para localizar
– vetores unitários usados para localizar ![]()
![]() – vetores unitários usados para localizar
– vetores unitários usados para localizar ![]()
![]() ,
, ![]() – perturbação de
– perturbação de ![]() ,
, ![]()
![]() ,
, ![]() – velocidades de
– velocidades de ![]()
![]() ,
, ![]() ,
, ![]() ,
,
![]() – velocidades angulares de
– velocidades angulares de ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() – ponto fixo em
– ponto fixo em ![]()
![]() – vetor posição de
– vetor posição de ![]() em relação a
em relação a ![]()
![]() ,
, ![]() ,
, ![]() – coordenadas de
– coordenadas de ![]()
![]() – raio de giro constante
– raio de giro constante
![]() – trail
– trail
![]() – valor especial constante de
– valor especial constante de ![]()
Referências
[1] ROLAND, R. D. “J. Mech. Engng Sci”, (1971), p. 316.
[2] WHIPPLE, F. J. W. “Qt. J. Pure Appl. Math.”, 30, (1899), p. 312.
[3] BOWER, G. S. “Automobile Engnr”. Em: V, (1915), p. 280.
[4] PEARSALL, R. H. “Proc. Inst. Automobile Engnr”. Em: XVII (1922), p. 395.
[5] WILSON-JONES, R. A. “Proc. Inst. Mechanical Engineers, Automobile Division”, (1951-2), pp. 191–199.
[6] SHARP, R. S. “J. Mech. Engng Sci”, 13, (1971), p. 316.
[7] ROLAND, R. D. “Mechanics and Sport”, American Society of Mechanical Engineers NewYork (1973), pp. 35–52.
[8] HUSTON, R. L. e PASSERELLO, C. E. “Matrix & Tensor Qt.”, (1973), pp. 109–112.


Deixe um comentário